BFS 문제 풀이법 정리
들어가며
최근에 BFS 유형의 문제에 익숙해지기 위해 백준에서 BFS 문제들을 풀어보았다. 문제를 풀면서 어려움을 겪었던 점이 있어 이를 설명하고 풀이 방법에 대해서 정리해볼 것이다. 코드는 파이썬을 기준으로 작성했다.
헷갈렸던 점
처음에 BFS문제를 풀면서 가장 헷갈렸던 부분은 언제 방문 체크를 해야하는지였다. 기존에 알고있던 BFS의 동작방식과 내가 블로그에서 찾았던 코드들의 구현방법이 달랐기 때문에 그랬던 것 같다.
1
2
3
4
5
6
7
8
9
10
# 대략 내가 찾았던 코드의 동작 예시
visited = [] # 방문한 곳을 저장할 저장소
queue = deque([root])
while queue:
value = queue.popleft() #꺼내고(dequeue)
if value not in visited: #방문하지 않은 것이면
visited.append(value) #방문 처리하고
queue += (set(graph[value]) - set(visited)) #queue에 enqueue
많은 블로그에서 위처럼 dequeue를 할 때 방문체크를 하고 if 문을 통해 중복으로 enqueue된 값을 거르는 방법을 알려주었는데, 곰곰이 생각해보니 꼭 그럴 필요가 없다고 생각이 들었다.
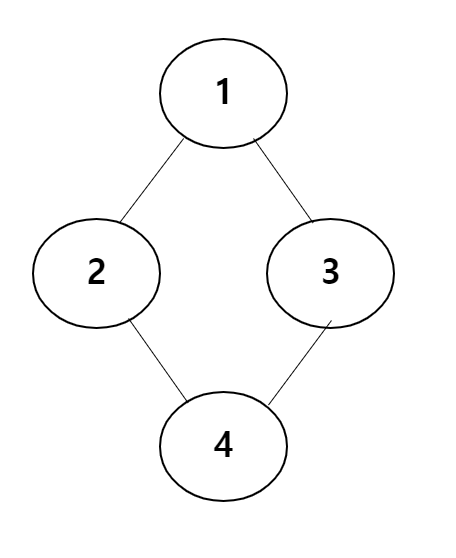
예를 들어 위와 같은 방법(dequeue시 방문체크)으로 위 그래프를 1번부터 방문 한다면 queue에 들어가는 순서는 다음과 같을 것이다.
1 - 2 - 3 - 4 - 4
위에 4번 노드가 2번 들어간 것 처럼 queue에 방문할 데이터가 중복으로 들어가는 경우가 생길 수 있고 이는 트리 관계가 복잡해질 수록 중복이 많아진다.
물론, 이를 visited에 있는지 확인을 통해 중복데이터를 거르긴 하지만 처음에 enqueue할 때 방문체크를 해버리면 불필요하게 중복으로 넣었다 뺄 필요가 없다고 생각했다.
그래서 enqueue시에 방문체크를 하는 방법이 더 직관적이고 효율적이라고 생각이 들어 나는 이 방법으로 구현을 하기로 했다.(물론 위의 방법이 틀린 것은 아니다.)
BFS 구현하는 법
대략적인 동작방식은 다음과 같다.
- 갈 곳을 queue에 넣는다.(root를 enqueue)
- 갈 곳에 방문 체크를 한다.(visited에 추가)
- queue에서 dequeue를 하여 가장 먼저 방문할 노드를 꺼내온다.
- 갈 수 있는 곳에서 이미 갔던 곳(visited에 추가된 곳)을 제외하고 다시 queue에 넣는다.(1번과 같은 enqueue작업)
- 2~4과정을 반복한다.
위를 파이썬으로 구현한 코드는 다음과 같다.
1
2
3
4
5
6
7
8
9
10
11
root = 1
visited = set([])
queue = deque() #'from collections import deque'선언 필요
queue.append(root)
visited.add(root)
while queue:
value = queue.popleft() # 꺼내기(dequeue)
queue += graph[value] - visited # 방문할 곳 넣기(enqueue), graph와 visited 둘 다 set
visited.update(graph[value] - visited) # 방문체크(set이면 굳이 visited를 안빼도 됨)
위의 코드에서 눈여겨 볼 점이 또 두 가지가 있다.
1. 라이브러리를 통해 deque를 사용
- 파이썬에서 pop(0)을 통해서도 dequeue동작을 할 수 있지만 연결리스트로 구현된 deque의 popleft()를 이용해 dequeue동작의 시간복잡도를 O(n)에서 O(1)로 줄일 수 있다.
2. set 활용
- enqueue 동작을 할 때 visited에 있는 노드를 제외한 노드들을 넣어야하는데, 각 노드는 유일하기 때문에 visited나 graph에서 중복된 정보를 가질 필요가 없다.
- 따라서 set을 이용할 수 있는데 set을 이용하면 차집합을 간단히 구현할 수 있어 편리하다.
⚠️주의 set은 순서가 보장되지 않기 때문에 간선간 가중치가 있거나 경로를 알아야 하는 경우에는 적합하지 않다.
깊이를 카운팅 하는 법
위의 문제에서 최단거리를 구해야 했는데 ‘최단거리 == BFS로 첫 탐색의 깊이’이기 때문에 깊이를 구해야 했다.
처음에 반복문에 카운팅도 해보고 여러가지 시도를 해봤지만 잘 되지 않았다. 그래서 방법을 찾아보았는데 의외로 간단했다.
enqueue를 할 때 카운팅하며 같이 저장을 해주면 된다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 미로 탐색 제출코드 중 BFS 부분
queue = deque()
queue.append((0,0,1))
map[0][0] = '0'
count = 0
while queue:
# queue에서 빼오고 표시
p = queue.popleft()
n,m,c = p
## print(n,m)
if n == N-1 and m == M-1:
print(c)
break
# 갈 수 있는 곳 queue에 넣고 방문체크
if n < N-1 and map[n+1][m] == '1': #아래로 한칸
queue.append((n+1,m,c+1))
map[n+1][m] = '0'
if m < M-1 and map[n][m+1] == '1': #오른쪽 한칸
queue.append((n,m+1,c+1))
map[n][m+1] = '0'
if n > 0 and map[n-1][m] == '1': #위로 한칸
queue.append((n-1,m,c+1))
map[n-1][m] = '0'
if m > 0 and map[n][m-1] == '1': #왼쪽 한칸
queue.append((n,m-1,c+1))
map[n][m-1] = '0'
2차원 공간에서의 BFS
위와 같은 2차원 공간의 탐색 문제를 많이 접할 수 있는데 이를 그래프의 관점에서 보고 BFS로 구현할 수 있다. (특히 최단거리 문제)
일반적인 N*M의 2차원 공간이 주어진다면, 각 칸이 노드이고 상하좌우로 양뱡향 연결이 되어 있는 것으로 생각할 수 있다.
구현 방법
각 상하 좌우의 범위가 인덱스를 넘지 않는지를 먼저 판단하여 접근 여부를 확인하고, 그 다음 갈 수 있는 곳인지를 판단(방문여부 판단)한 뒤 갈 수 있다면 queue에 넣고 방문 체크를 한다.
방문 체크 방법
이 때 방문 체크를 어떤식으로 저장할지도 중요해지는데 visited에 그냥 좌표를 넣을 경우 또 탐색을 해야하기 때문에 방문 여부를 탐색하는 시간복잡도가(V*E)가 된다.
이를 최적화 하기 위해, 미리 2차원 공간을 만들어 방문 여부를 체크하면 시간복잡도를O(1)로 줄일 수 있다. 위 같은 미로문제에는 2차원 공간이 미리 주어져 있기 때문에 이를 이용하여 체크하면 된다.
사실 이건 2차원 공간 뿐만 아니라 모든 그래프에 적용할 수 있다.
정리
- 방문 체크는 enqueue와 동시에 하자
- enqueue 동작은 deque의 popleft()를 사용하자
- 경우에 따라 set을 잘 활용하자
- 깊이는 enqueue시 카운팅 하여 구할 수 있다
- 2차원 공간도 그래프로 볼 수 있다
시간이 오래 걸린다면 방문체크에 메모리를 적극 활용하자
지금까지 BFS문제를 풀면서 알게된 점에 대해서 정리를 해봤다. 아직 많은 문제를 풀어보진 않았지만 그래도 BFS문제를 푸는법에 대해서는 대략적으로 알게된 것 같다.
다음에는 동적 프로그래밍 유형의 문제를 풀어보고 정리를 해봐야겠다.
잘못된 정보가 있으면 언제든지 지적해주시길 바랍니다!🐥